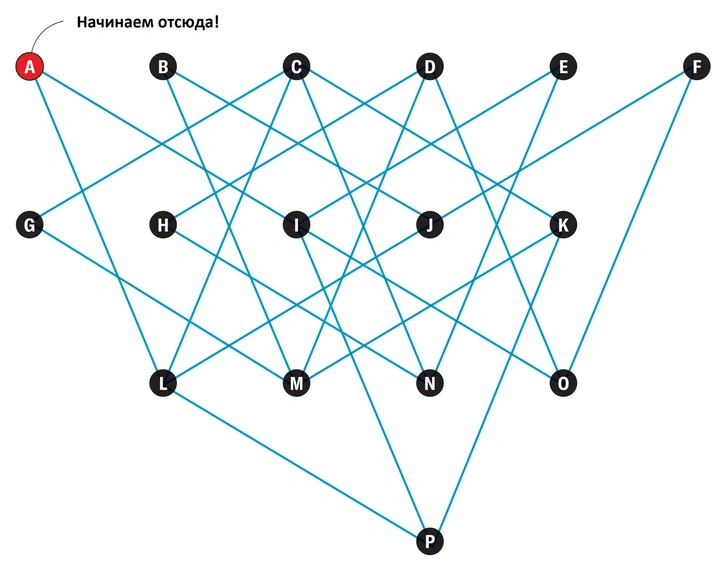
Продавец, живущий в городе А, хочет в течение недели посетить все города от B до P, но не обязательно в алфавитном порядке. В конце своего путешествия ему надо вернуться в A.
Важный нюанс: продавец планирует посетить каждый город только один раз.
Синие линии — единственные дороги, соединяющие 16 городов.
Продавец может использовать только прямой маршрут между любыми двумя городами, то есть ему нельзя поворачивать на пересечении двух улиц.
А теперь ответьте: сколько различных маршрутов возможно?
Задача
- Источник:
Генри Дьюдени «Пятьсот двадцать головоломок» (1917)
Пока продавец идет, можете гадать задачку. Но не спешите листать низ. Как только продавец придет к правильному ответу, у вас не останется возможности найти решение самостоятельно!
🚶🏻♂️
🚶🏻♂️
🚶🏻♂️
🚶🏻♂️
🚶🏻♂️
🚶🏻♂️
Вы уже совсем близко к отгадке. Не листайте дальше, если хотите еще подумать!
🚶🏻♂️
🚶🏻♂️
🚶🏻♂️
🚶🏻♂️
🚶🏻♂️
Итак, правильный ответ!
Если продавец въезжает в город по одной дороге, он должен покинуть его снова по другой. Путешествие туда и обратно состоится, если в каждый город ведут как минимум две дороги.
В города A, B, E, F, G и H ведут ровно две дороги. Следовательно, продавец должен путешествовать по этим дорогам, несмотря ни на что. Это также определяет, какие дороги он будет использовать, чтобы добраться до городов I, J, M и N и покинуть их.
Тогда остальные соединения также будут ясны. Следовательно, у продавца есть только один возможный путь туда и обратно — AIENHDOFJBMGCKPLA. Смотрите сами:
Решение
- Источник:
Генри Дьюдени «Пятьсот двадцать головоломок» (1917)
