- Источник:
- New York Times
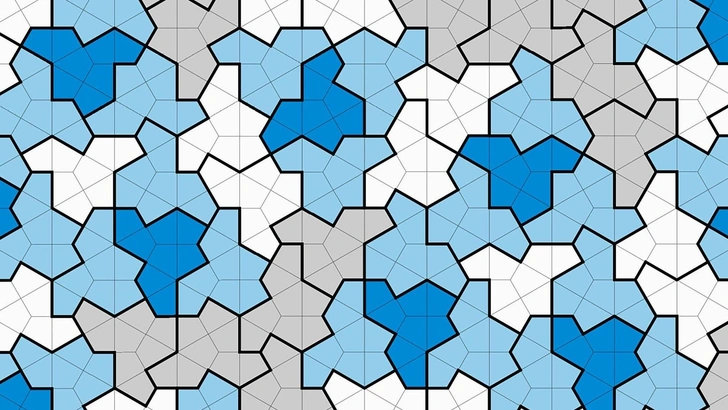
Английский математик-любитель Дэвид Смит решил задачу, которая вызывала споры более 60 лет — нашел неуловимого эйнштейна. Речь о фигуре, которая может бесконечно образовывать на плоской поверхности узор, который никогда не повторяется. Ранее такие рисунки удавалось составить только из нескольких форм. Автор назвал фигуру шляпой, так как она похожа на головной убор.
Один камень для бесконечности
На языке математиков «шляпа» Смита — это апериодический монотиль, который покрывает плоскость или бесконечную двухмерную поверхность, но без повторения рисунка. Специалисты поясняют: обои или кафельный пол могут быть частью бесконечного рисунка, но если его скопировать и сместить, он окажется точно наложен на самого себя и будет периодически повторяться.
Апериодическая мозаика не имеет такой симметрии. Математики долго искали единственную форму, которая могла бы выложить плоскость таким образом — это известно, как проблема эйнштейна (по-немецки ein stein — это один камень или одна плитка).
«Шляпа» имеет 13 сторон и представляет собой поликит — форму, построенную из восьми четырехугольников, похожих на воздушных змеев. По словам Смита, работу он вел в основном вручную, только в самом начале рисовал фигуры в простенькой программе на компьютере. Если какая-то из них казалось ему перспективной, математик вырезал на станке 32 таких силуэта и начинал «кружить» с ними на полу, выкладывая паззл без зазоров и перекрытий.
«Вы буквально ищете что-то одно на миллион. Отфильтровываете 999 999 скучных фигур, чтобы получить что-то заслуживающее дальнейшего изучения. Затем вручную изучаете и начинаете извлекать структуру. Вот где компьютер бесполезен: человек должен был участвовать в построении доказательства, которое только человек мог бы понять».
Чтобы подтвердить , Смит проконсультировался с профессиональными коллегами. Они проверили плитку с помощью вычислительного алгоритма, который генерировал огромные плоскости с узорами.
Задачка для пытливых умов
До сих пор существование апериодического монотиля было исключительно теоретическим и вызывало большие сомнения. В 1961 математик Хао Ван считал, что создать такой узор невозможно. Его ученик Роберт Бергер опроверг это утверждение, но он создал набор из 20 426 плиток! Затем — из 104. Об одной плитке речи тогда не шло.
Однако открытие Бергера положило начало соревнованию, и уже в 1970-х физик-математик из Оксфорда нобелевский лауреат Роджер Пенроуз представил свои две плитки для узора. С тех пор вариантов с двумя формами появилось несколько. Но никто не мог найти одну-единственную. «Шляпа», по словам ученых, не новая геометрическая фигура и не изобретение Смита. Но, видимо, никто прежде не рассматривал ее для решения проблемы эйнштейна.
